虚数空間の万華鏡
👤伊藤径

潜在性の源泉としての虚数空間

「根のない木を土に挿したものは生気がない。根の深い木には生気が充実している。またこういうことを造園師から聞いた。庭にある石は唯石を地上に置いただけでは力がない。その石の地中に埋まっている部分が、深ければ深いほど力がある、と。私が古くから言っておる“余韻ある俳句”という事もまた“背景ある俳句”という事も皆この地下に犇いている感情、若しくはその因果、事実の連続等をいうのである」とは、客観写生の神髄を説いた俳人・高浜虚子の言葉です。

冒頭の俳人・虚子の言葉と次の「虚数の世界」の話が奇妙にシンクロしているので、ご紹介します。

虚数ⅰと実数１の関係は、氷山と海の関係に喩えることが出来る。私たちが「現実」として直接観測できる実数（物体や結果）は、海面上に現れている氷山の一角（実部）に過ぎない。しかし、その氷山の安定性や大きさの部分は、海面下に隠された巨大な部分（虚部、潜在性）によって支えられており、虚数ⅰは、この目に見えない、しかし不可欠な海面下の構造を記述するための座標軸を果たしている、といえる。

虚数が生まれたのは、古代ギリシャ時代から続く「方程式の解を求める」という人類の探求の歴史が深く関係しています。特に、16世紀のイタリアで、それまで誰も解けなかった難しい方程式に挑んだ数学者たちの熱意が、虚数発見の大きな原動力となりました。数学者ボンベリは、実数解しか持たない３次方程式を解く過程で、√-1 の計算を経由しなければならないという問題に直面しました。彼は、この本来は 「実在しない数」が「実在する解」を得るための一時的な「架空の計算領域」として必要悪であることを示しました。このボンベリの発見の核心は、「観測不可能な虚数を含む状態（潜在性）」が、「観測可能な実数の結果（現実）」を生み出すという量子の構図を、300年以上も早く予見していたかのようである、と指摘されています。

つまり虚数は、現実とその背後に隠れた潜在性を結ぶ記述システムであるとする考え方です。虚数ⅰが、我々の直感（一次元の実数）では捉えきれない世界の「隠れた側面」や「もう一つの次元」を記述するために必須の言語であるということです。

その最も根源的なレベルで数学と現実が深く結びついているのは、世界の最小単位を記述する量子の世界です。量子の基本方程式であるシュレディンガー方程式（左上式）に虚数ⅰが本質的に含まれています。

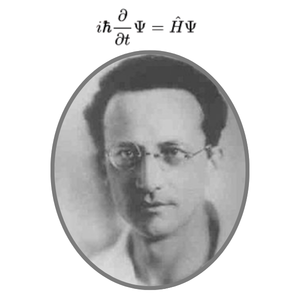
量子力学の世界において、虚数単位ⅰ は、単なる計算上の便益ではなく、世界の「記述の根幹」そのものであるとされています。虚数ⅰ は、我々の直感が捉える実数（1次元）では記述しきれない、世界の「もう一つの次元」を記述するために発見された「最も強力な言語」であり、量子の世界では特に「潜在性（まだ現実化していない可能性）」の記述子として機能します。ⅰ を含まない実数の範囲だけでは、この量子の世界を記述すること自体が不可能です。

粒子の位置情報を持つ「波動関数 ψ 」は、物理的に直接測定できず、その値は複素数（複素関数）です。近年の哲学的解釈では、複素数 z=a+bi の構造が、量子力学の根幹にある「現実—潜在性 (reality-potentiality)」
という物理的二重性に対応していると提唱されています。実部 a は 観測され、確定した「現象（現実）」、すなわち実数として認識できる世界を記述します。虚部 bi は、観測されておらず、複数の可能性が「重ね合わされた」状態、すなわち「潜在性 (potentiality)」を記述します。

この解釈に基づくと、虚数 i  は「まだ現実化していない状態」そのものを表す「記述子」として機能しています。電子が「波動関数 ψ（虚数を含む）」として潜在的に存在し、「観測（∣ψ∣^2）」によって「実数の位置」が確定するというプロセスは、この虚数（潜在性）が実数（現実）を生み出す構図を示しています。波動関数 は、粒子が「どこにいるか」という情報を持つ「確率の波」を表します。 我々が観測できる「現実」との接続（粒子を発見する確率）は、波動関数 ψ の絶対値の2乗、すなわち∣ψ∣^2 によって与えられます。これにより、虚数を含む波動関数から、観測可能な実数値（確率）が導かれます。

したがって、量子の世界における虚数 i は、「潜在性と確率」を記述するための、現実そのものを構成する量子力学の根幹的な要素であると言えます。

そろそろここでオイラーの公式が登場しても良いころ合いかと思います。18世紀の数学者レオンハルト・オイラーが発見した公式で、世上、人類の至宝だと称されています。

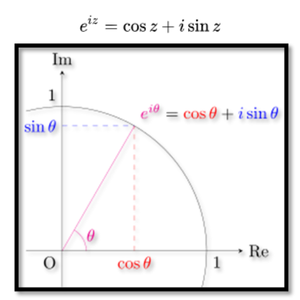
オイラーの公式の図形的な表現。複素数平面において、複素数 eiθ は、単位円周上の偏角 θ [rad] の点を表す

何故、この公式（右上式）が「人類の至宝」であり「すべての数学のなかでもっとも素晴らしい公式」だと言われているのかには理由があります。この公式は、オイラーが純粋に数学的な演繹と美しさを求める過程で発見したものです。この公式は、指数関数と三角関数を直接結びつけています。

まず左辺の e は、ネイピア数と呼び、生物の成長（細胞分裂による増殖）や利子の計算など「指数関数的な変化」を記述するものです。オウム貝や渦巻き銀河も指数関数的な変化を示す対数螺旋という美しい姿をしています。

一方、右辺の cos や sin は、円運動や波の振動など「周期的な変化」を記述するものです。それは絶えることのない動きの中にある。寄せては返す波、満ちては引く海の潮。片や細胞分裂、片や波動の生態、その本来異質な変化を示す左辺と右辺を等式で結びつけているのが、虚数iというわけです。生物の細胞分裂などの指数関数的な変化と一方は波の運動などの周期的な変化とが、どうして虚数iによって結びつくのか、不思議な気がします。それらがマジックのように結びつく。オイラーの公式の持つ意味を、複素平面上の幾何学的な動きで捉えると、その公式は、複素数に指数関数という「運動」の概念を結びつけたとも言えます。複素平面は、虚数 i を「静的な90度回転」と定義しましたが、オイラーの公式は e^iθ を「複素平面の単位円上を、角速度 θ で連続的に回転する運動」として記述することを可能としました。静態から動態へ進化したわけです。従ってオイラーの公式により、三角関数の sin と cos のペアは、e^iwt という「単一の複素指数関数」として扱うことが可能となりました。

この複素数による表現は、波の本質的な情報である「振幅（大きさ）」と「位相（タイミングのズレ）」という二つの情報を一つの数の中に分離して保持できる完璧な数学的ツールであり、フーリエ解析への道を開くなど、現代工学における多くの革新の根幹となっています。

オイラーの公式の意義について、ＡＩと交信すると、美しい詩的な答えが返ってきました。オイラーの公式を理解するために、「異なる楽器を完璧に調和させる指揮者」を想像してみてくださいと語り始めます。そうして見事な比喩で、われわれを高みへ誘います。

「成長」を奏でるバイオリン（指数関数）と、「振動」を刻む打楽器（三角関数）は、一見すると別の曲を演奏しているように見えます。しかし、オイラーの公式という「虚数のタクト（指揮棒）」が振られるとき、これら二つは一つの壮大なシンフォニーとして見事に融合します。この公式は、バラバラに見える自然界の法則を一つの美しいメロディへとまとめ上げる、究極のスコア（楽譜）なのです。・・とＡＩは語り掛けます。

オイラーの公式が生まれた経緯をもう少し哲学的に考えると不思議な感覚を覚えます。オイラーは、自分が発見したこの公式を、発見するずっと前から自然界に存在していたものだ、それはずっと前から分かっていたと不気味な予言者のような言葉を残しています。オイラーが導き出した公式が、後に電磁気学や量子力学、信号処理といった分野で、波の動きや電気回路の挙動などを説明するために不可欠なツールとなっていることからも、その信憑性がうかがえます。これは、あたかも数学が宇宙に刻まれた設計図を読み解く言語であり、数学者はその言語を解読する探求者であるという見方です。

ここで冒頭に述べた俳人・高浜虚子の言葉にシンクロするもう一つの言葉を紹介します。20世紀初頭に活躍した作家のヴァージニア・ウルフの言葉。ウルフが子供時代に経験し、生涯忘れられなかった印象深い体験を述べたエッセイです。

私は正面玄関のそばの花壇を眺めていた。「あれが統一なのだ」と私は言った。私はよく葉の茂った植物を見つめていた。とつぜん、花そのものが大地の一部であることが明白に思われた。一つの環が花であるものを取り巻き、それが本当の花で、一部は大地であり、一部は花なのだとはっきり思われた。

（「過去のスケッチ」『存在の瞬間』）

「一つの環が花であるものを取り巻き、それが本当の花で、一部は大地であり、一部は花なのだとはっきり思われた。」の言葉は、また、先に述べた「虚数 ⅰ と実数 １ の関係は、氷山と海の関係に喩えることが出来ます。私たちが「現実」として直接観測できる実数（物体や結果）は、海面上に現れている氷山の一角（実部）に過ぎない」とも奇妙にもシンクロします。本当の花を形成しているのは、それを取り巻く一つの環であり、統一体だとウルフは述べていますが、その言葉は虚数と実数との関係にシンクロします。我々の目の前にはっきり現れている実数は、虚数空間の氷山の一角が現れているに過ぎない、それを取り巻いている海のような存在の虚数空間を含めて全体、統一体であると数学者や物理学者たちは、哲学的な考察を深めているようなのです。彼らは、虚数空間としての「真の現実」を語ります。「真の現実」とは、測定できる実数（現象）だけでなく、観測される前の「虚数空間」に潜在しているあらゆる可能性をも含んでいると見なします。

なぜ、この量子たちが棲息する世界の根源的な法則が、「実在しない」はずの虚数 i を含まねばならないのか？と彼らは自問し、そうしてこの深遠な問いに対し、近年の物理学および哲学では、複素数の本質に迫る考察が進められています。先に述べたように複素数は、z=a+bi という、実部と虚部の二つの要素が対になった構造を持ちます。

この数学的二重性が、量子力学の根幹にある「現実―潜在性」や「観測による崩壊」「重ね合わせ現象」といった物理的二重性と驚くほど正確に対応しているのではないかと述べます。実部は、観測され、確定した「現実」。それは我々が測定し、実数として認識できる世界。一方虚部は、観測されておらず、複数の可能性が「重ね合わさった」状態、すなわち「潜在性」が内包された世界。この解釈において、「真空」とは単なる無では無く、あらゆる可能性が虚数空間に「潜在している」場、すなわち「虚数空間」として記述されるべきものだと提案されています。